Week #10: Towards a new Bubble Detection algorithm

This week was mostly focused on studying the paper named Superbubbles, Ultrabubbles, and Cacti by Benedict Paten et. al (which can be found here) in order to improve the bubble detection capabilities of my script. As you may remember from last week, VCF validation didn't go as expected, and I think Bubble Detection may be (at least part of) what's causing the issue. So, I was suggested to use that paper as a reference for a new, more general, Bubble Detection algorithm.

The current approach, which is heavily inspired by Flavia95's work, albeit with a few changes (such as using a BFS instead of a DFS), has two main drawbacks:

1. It is impossible to detect multiple (simple) bubbles that happen at the same distance from the root. This is due to the algorithm looking for a single node at a given level. This is clearly not the case when multiple bubbles are open at the same time.
   
   
2. It does not detect superbubbles properly. While there is a simple way to detect when a bubble is opening, it's harder to tell when it must be closed.

An example of a problematic graph

The approach presented in the paper is completely different. Instead of using a BFS-tree, it uses a completely different data structured called cactus graph. A cactus graph is a particular type of graph in which edge belongs to at most a single cycle (more information can be found here). The general idea is to convert the starting graph into a cactus graph, and then the cactus graph into a bridge forest.

In order to fully understand this paper, it is important to notice that the starting graph is represented as a biedged graph, that is a graph with two types of edges (black and gray), such as each vertex is incident with at most one black edge. With regards to the Handlegraph model, a black edge in a biedged graph is equivalent to a node; a grey edge is instead equivalent to an edge. While this conversion may appear to be straightforward, in practice is makes the algorithm not so easy to translate between the two.

In order to obtain the bridge forest from a given biedged graph, the following steps must be followed:

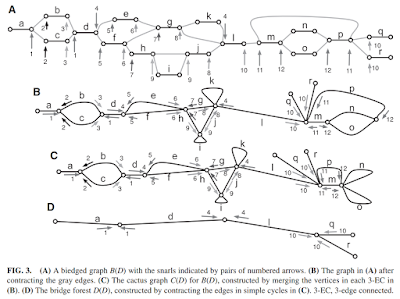
1. Contract the grey edges in the biedged graph 
2. Merge the vertices in each 3-edge-connected component, to obtain a cactus graph 
3. Contract the edges in each cycle, to obtain a bridge forest 

Bridge forest construction algorithm illustrated

The main problem with applying this algorithm to a Handlegraph instead of a biedged graph is that in step 1 the grey edges get "eliminated" (or rather, contracted) so that only black edges remain. But what does this entail in a Handlegraph? It can't be multiple nodes because there is no edge (grey edge in the biedged graph) connecting them; it also makes no sense to have a single node representing the whole graph. This is still an open issue, and I'll try to solve it by taking a close look at how vg implements this algorithm.

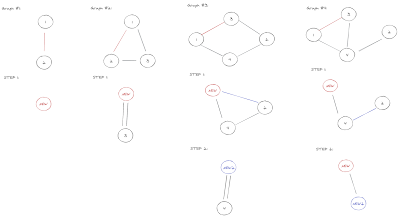My take on simulating step 1 of the algorithm above, but is it actually correct?